CalculateCamScreenDV()

Purpose: To update the camScreenDV (Cam Screen Displacement Vector). It calculates this using the current camRO (Camera Rotation Orientation) and the camCoords (The camera’s X, Y and Z coordinates).

It's ultimate goal is to find the length of the line segment below highlighted with a red squiggly line.

There exists a point on the camera where the normals vector from the origin [0,0,0] hits the camera screen. This vector is always perpendicular to the camera screen (hence its called the normals) The red squiggly line represents the distance between the center of the camera screen and the point where this normals vector lands.

In diagram 1.1 below, we can get the length of the red squiggly line (the CamScreenDV) by finding Angle B and DistToOrigin (Distance from the camera to the origin[0,0,0]).
Cos(Angle B) = CamScreenDV / DistToOrigin.
Therefore CamScreenDV = Cos(Angle B) * DistToOrigin

Finding DistToOrigin is easy but finding Angle B is slightly more complicated

Process:

Step 1: Calculate Distance from Camera To Origin[0,0,0]

Use the Pythagorean theorem to find the distance from the camera to the origin[0,0,0]. The camera's coordinates will tell you how much the camera has displaced from the origin on each axis. Eg: If the camCoords are [-4, 0, -2], this means it has displaced -4 on the X-axis and -2 on the Z-axis. So the vector that both of these individual displacements have created is the distance from the camera to the origin. And we get that by calculating: √((X-Displacement)² + (Y-Displacement)²)

Note: Remember to keep in mind that since you're looking at things from the top view, the local Y-axis of the top view corresponds to the Z-axis of the actual 3D space.

Step 2: Calculate Angle Between CamXPlane and the DistToOrigin Vector

We now have the DistToOrigin vector. In order to eventually get Angle B, we can use the following approach. Notice the angle drawn in dark blue. This is the angle between CamXPlane and the current position of the camera (rotation orientation wise). This angle is clearly CamRO. It would be non existant if the CamRO was 0 since the cam would be parallel with the CamXPlane. It's directly proportional to the CamRO.

Now look at the angle drawn in light blue (Which we'll call Angle T). This is the angle between the CamXPlane and the DistToOrigin vector. If we can find this angle, then we simply have to substract CamRO from it and then we get Angle B.

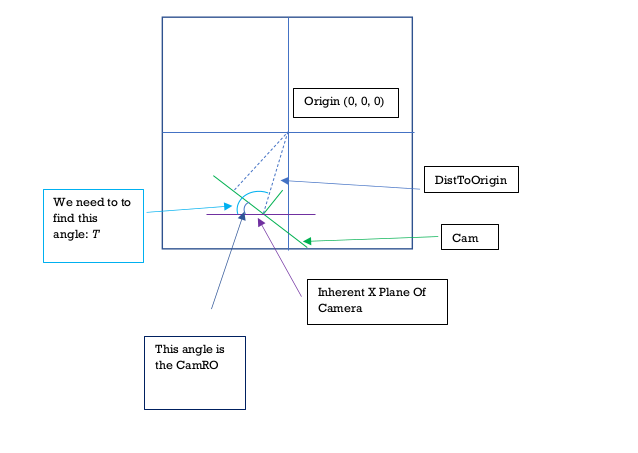
Angle T forms a non-right angled triangle. So we can't use SOH CAH TOA. We'll have to get creative.

Let's revisit the displacement of the camera from the origin[0,0,0]. Dissect the displacement for each axis. Pretend you're holding a pen which is on the origin[0,0,0]. Now slide the pen left or right to track the X-Axis displacement of the cam. Then slide the pen up or down to track the Z-Axis displacement. Once you're done, STOP. The pen is now on the camera. If you draw a line straight to the origin, you'll get the DistToOrigin vector. But notice how we now have a right angled triangle? (The X-axis displacement, Z-axis displacement and the DistToOrigin vector). Within that triangle we now have an Angle X. We can easily find that out with Tan inverse. Tan(Angle X) = (X-Axis Displacement) / (Z-Axis Displacement).

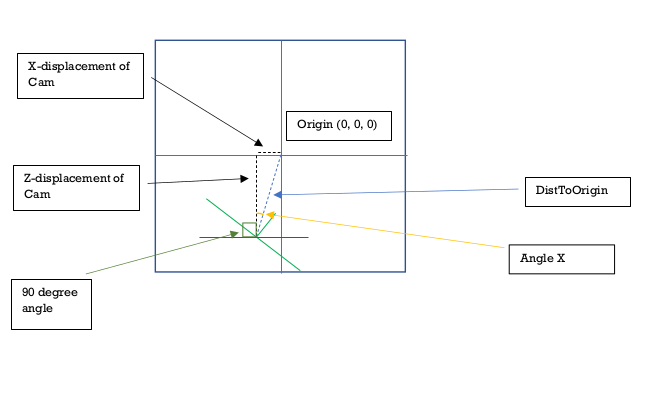
Now notice how the angle between CamXPlane and the start of Angle X is 90 degrees? The start of Angle X represents the Z-Axis line. Which means if we add 90 degrees (which is PI/2 in radians) to Angle X, we can finally get Angle T.

Step 3: Get Angle B

Now to get Angle B, we just have to subtract CamRO from Angle T. And then we get the DV with the equation we discussed in the beginning. CamScreenDV = Cos(Angle B) * DistToOrigin;